
Please Note: Balanced Assessment printed materials are available from this site, except for those indicated below. Please use the order form and follow the ordering directions carefully as they have changed. Current prices can be found on our order form.
Please also note that the Balanced Assessment
Primary &
Elementary Tasks have been published by Corwin
Press. The Balanced Assessment Transition & Middle School Tasks have been published by Teachers' College Press. These tasks may still be viewed
in .pdf
format on this website but they may not be copied or printed.

![]()
![]()

![]()
![]()
![]()
An Interim Report
of the
Harvard Group
Balanced Assessment in Mathematics Project
September, 1995
Educational Technology Center
Harvard Graduate School of Education
This research was supported by a subcontract from the University of California at Berkeley, under National Science Foundation grant MDR‑9252902.
Let early education be a sort of amusement; you will then be better able to find out the natural bent.
Plato, The Republic, bk. VII, 537
Introduction
Assessing the mathematical performance of our students and the effectiveness of our mathematics instructional programs has become a major concern of a large part of the mathematics education community as well as a concern of several larger publics. The National Council of Teachers of Mathematics (NCTM) has addressed that concern in its recently released Assessment Standards for School Mathematics which provides a set of six standards to guide the development of assessment instruments for school mathematics.
This NCTM document makes clear, however, that it is a guide and not a “how-to” document. Guides are necessary but not sufficient. One actually needs different models of assessment that instantiate the principles set down in guidelines such as those offered by the NCTM. Balanced Assessment in Mathematics (BA) is a National Science Foundation Project charged with developing new approaches to the assessment of mathematical competence in the elementary and secondary grades. The principal grantee is the University of California at Berkeley with subcontracts to Michigan State University, the Shell Mathematics Centre of the University of Nottingham, and the Educational Technology Center of the Harvard University Graduate School of Education. The Principal Investigator for the entire project is Alan Schoenfeld of the University of California at Berkeley.
The main goal of Balanced Assessment is to produce assessment that can be used in classrooms throughout the nation — assessments that reflect the values of the mathematics reform movement as articulated in the National Council of Teachers of Mathematics Curriculum and Evaluation Standards. The assessments created by Balanced Assessment are designed to provide students, teachers, schools and parents with useful information about how students and programs are doing with respect to those standards.
This document is an interim report of two years of work by the Harvard Group of the project. It is intended to both complement and supplement other reports issued by the project. This report addresses the following questions:
· What is mathematics about?
· What are the purposes of assessment?
· How should assessment in mathematics be done?
· What is Balanced Assessment in Mathematics about?
· What is the Harvard Group of Balanced Assessment in Mathematics about?
Our report also includes a complete archive of the work of the Harvard Group. It contains a packet of on-demand tasks and scoring rubrics at the elementary level, several packets of on-demand tasks and scoring rubrics at the secondary level, a secondary level portfolio packet containing problems and projects, and a technology resource package from which teachers may draw materials to supplement other on-demand assessment. Included with this report is a CD-ROM containing all of these materials in a form that can be used by anyone who has access to Microsoft Word on either a PC-compatible or Macintosh computer with a CD-ROM drive.
The work of the Balanced Assessment Project has been influenced in no small measure by the efforts of those who preceded it. We have been helped enormously by being able to draw on these efforts. A selected bibliography of the most important of these is included as Appendix C.
This document owes much to the work of many hundreds of students and dozens of teachers. We are indebted to all of them. We are particularly grateful to Joel Hillel for helping us think through many knotty issues. In addition we want to thank Walter Stroup and the Boston teachers and students with whom he worked for many of the tasks involving graphing calculators. Finally, we wish to thank our colleagues at the other project sites.
Judah L. Schwartz, Director
Joan M. Kenney, Coordinator
Kevin A. Kelly
Teresa Sienkiewicz
Yesha Sivan
Victor Steinbok
Michal Yerushalmy
Table of Contents
1. What is Mathematics About? — the way we see the structure of the subject...............
The Objects of Mathematics..................................................................................................
The Actions of Mathematics................................................................................................
What Can/Should be Expected of Students at the Elementary Level.......................................
What Can/Should be Expected of Students at the Secondary Level.......................................
2. What are the Purposes of Assessment?...........................................................................
3. How should Assessment in Mathematics be Done?.........................................................
4. What is Balanced Assessment in Mathematics About?...................................................
5. What is the Harvard Group of Balanced Assessment About?........................................
Why this Report?................................................................................................................
Task Design........................................................................................................................
New Task Types.................................................................................................................
The “-Ness” tasks.........................................................................................................
Fermi tasks....................................................................................................................
Example generation........................................................................................................
Weighting of Tasks..............................................................................................................
Writing Rubrics for Tasks....................................................................................................
Scoring Student Performance...............................................................................................
Balancing Assessment Packets.............................................................................................
Appendix A: Mathematical Content Matrix for the Elementary Grades..........................
Appendix B: An Analysis of the “Square-Ness” Task........................................................
Appendix C: Selected Assessment Bibliography.................................................................
Appendix D: Balanced Assessment Packets........................................................................
A Balanced Assessment Packet for the Elementary Grades....................................................
Balanced Assessment Packets for the Secondary Grades......................................................
The Technology Resource Packet........................................................................................
Like many subjects, it is possible to identify both content and process dimensions in the subject of mathematics. Unlike many subjects where most of the process dimension refers to general reasoning, problem-formulating and problem-solving skills, the process dimension in mathematics refers to many skills that are mathematics specific. As a result, many people tend to lump content and process together when speaking about mathematics, calling it all mathematics content.
We believe it is important to maintain the distinction between content and process. In part we say this because we believe that this distinction reflects a something very deep about the way humans approach mental activity of all sorts. All human languages have grammatical structures that distinguish between noun phrases and verb phrases. They use these structures to express the distinction between objects, and the actions carried out by or on these objects.
We believe that the content-process distinction in mathematics is best described by the words object and action. What are the mathematical objects we wish to deal with? What are the mathematical actions that we carry out with these objects? We will try to answer these questions in a way that makes clear the continuity of the subject from the earliest grades through post-secondary mathematics. Seen in the proper light there are really very few kinds of mathematical objects and actions.
The first set of mathematical objects we need to consider are number and quantity. Indeed, elementary mathematics is largely about these objects and the actions we carry out with and on them.
integers (positive and negative whole numbers and zero)
rationals (fractions, decimals and all the integers)
measures (length, area, volume, time, weight)
reals (p, e, etc. and all the rationals)
complex numbers
vectors and matrices
Along with number and quantity we introduce very early a concern for another kind of mathematical object, namely shape and space.
topological spaces (concepts of connected and enclosure)
metric spaces (with such shapes as lines/segments, polygons, circles, conic sections, etc.)
From the beginning we try to make students aware of pattern in the worlds of number and shape. Pattern as a mathematical object matures into function which is the central mathematical object of the subjects we call algebra and calculus.
functions on real numbers (linear, quadratic, power, rational, periodic, transcendental)
functions on shapes
There are several other kinds of mathematical objects that have less prominent roles in the mathematics we expect our youngsters to study. These include Chance and Data, and Arrangement:
relative frequency and probability
discrete and continuous data
Some aspects of data collection, organization and presentation can be done in the earliest grades but little, if any, data analysis. Notions of probability are not realistically addressable until late middle school.
permutations, combinations, graphs, networks, trees, counting schemes
At the youngest grades, these topics tend to blend with the study of patterns of numbers and shapes.
The following table describes the kinds of mathematical objects in more detail, along with their properties, operations that can be performed on them, and their pragmatic uses.
|
properties of objects |
operations on objects |
semantics of pragmatic use |
|
|
Number and Quantity integers rationals reals
measures: length area volume time weight |
order between-ness
part-whole relationships
units dimensions
|
arithmetic operations
addition subtraction multiplication division exponentiation |
counting or measuring anything in the world around us |
|
Shape and Space topological
metric: lines/segments polygons circles conic sections
other (e.g. spherical geometry) |
connectedness enclosure
distance location symmetry similarity |
scaling projection translation rotation reflection inversion conformal mapping homotopies/deformations covering, packing and tessellating |
designing and building objects
mapping and traveling |
|
Pattern and Function linear quadratic power rational periodic transcendental
|
domain/range continuity boundedness rate of change, curvature, etc. maxima and minima rate of accumulation
linear-root, slope/intercept
quadratic-roots, axis of symmetry
power-roots, asymptotic behavior
rational-roots, singularities, asymptotic behavior
periodic-frequency, phase
transcendental-“growth” constant |
arithmetic operations (functions on Rn)
comparison equations inequalities identities
composition translation reflection dilation/contraction
|
expressing how something depends on one or more other things
resolving constraints (solving equations and inequalities)
|
|
Chance and Data discrete continuous
|
determinism randomness relative frequency distribution moments |
sampling (by counts and/or measures)
composing representing |
dealing with uncertainty
dealing with lack of precision |
|
Arrangement permutations combinations graphs/networks trees |
adjacency enumeration vertices and edges of graphs/networks |
|
organizing discrete information |
As previously mentioned, the process dimension of mathematics has many actions that are mathematics specific. It also involves actions that are properly regarded as general problem-formulating, problem-solving and reasoning skills. We divide these skills into four categories.
Modeling/Formulating
Transforming/Manipulating
Inferring/Drawing Conclusions
Communicating
With the exception of communication, each of these actions has aspects that are specific to mathematics and aspects that are not specific to mathematics but that are quite general in nature. We list below some of these aspects.
observation and evidence gathering
necessary and/but not sufficient conditions
analogy and contrast
deciding, with awareness, what is important and what can be ignored
deciding, with awareness, what can be mathematized and then doing so
formally expressing dependencies, relationships and constraints
understanding “the rules of the game”
understanding the nature of equivalence and identity
arithmetic computation
symbolic manipulation in algebra and calculus
formal proofs in geometry
shifting point of view
testing conjectures
exploitation of limiting cases
exploitation of symmetry and invariance
exploitation of “between-ness”
making a clear argument orally and in writing (using both prose and images)
It is evident that there is no reasonable way to separate, nor should there be any interest in separating, the domain-specific and the domain-general aspects of the process dimension of mathematics. We therefore come to the conclusion that it is better to parse the domain of mathematics as
object (Number and Quantity, Shape and Space, Pattern and Function, Chance and Data, Arrangement)
´
action (including both domain-specific and domain-general actions)
rather than by
content (usually defined by “topics” — an undifferentiated mixture of objects and domain-specific actions)
and
process (i.e. domain-general actions)
which is the usual procedure in mathematics education.
We view elementary mathematics (at about the 4th grade level) as being concerned with the following mathematical objects:
number and quantity
shape and space
pattern
data
We expect youngsters to be able to demonstrate
· a robust understanding of the conceptual meaning of addition and subtraction of whole numbers and integers
Sarah has 3 apples and Joe gave her 2 more. How many
apples does Sarah have now?
Sarah has 3 apples and Joe has 2 more apples than Sarah. How many apples do
they have altogether?
· a growing understanding of the various meanings of both multiplication and division of whole numbers and integers
At a party 20 bags of candy were given out. Each bag
contained 5 candies. How many candies were given out altogether?
Thelma has 5 skirts and 3 blouses. How many different outfits can Thelma put
together?
· a reasonable degree of computational facility with the four arithmetic operations on whole numbers and integers
· an ability to make reasonable approximations for the results of arithmetic computations (this expectation is not currently realizable in most US fourth grade classrooms)
To the nearest hundred, what is 38 times 42?
To the nearest hundred, what is 716 and 879?
· a growing understanding of the order properties of decimals and other rational fractions (this expectation is not currently realizable in most US fourth grade classrooms)
Write a fraction that is larger than 1/3 and smaller
than ½.
Write a decimal that is larger than 0.083 and smaller than 0.15.
· an ability to identify and measure continuous quantity such as length, area, weight and time
· an ability to make reasonable estimates of lengths, areas, weights and time in ones environment
How much does a gallon of milk weigh?
How much time does it take you to say your name?
We expect youngsters to be able to demonstrate
· an ability to distinguish and name a variety of two- and three-dimensional shapes
Draw three different kinds of closed figures that have four straight lines
· an understanding of the symmetries of these shapes
Find all the lines along which you can fold a paper hexagon so that the two parts lie exactly on top of each other.
· an ability to read and interpret simple maps
Which two rooms in your school are furthest apart? Figure out three different routes that go from one to the other and tell how you would decide which is the shortest route.
We expect youngsters to be able to demonstrate
· an ability to recognize and generate numerical patterns
What numerical pattern could continue the sequence
1, 4, 7, 10, 13, ....?
What numerical pattern could continue the sequence 1, 2, 4, 8, ....?
· an ability to recognize and generate spatial patterns
Can you tile a floor with tiles like this so that the pattern is “regular”?
· an ability to enumerate and organize simple combinations and permutations
How many different ways can you seat four people at a square table so that there is one person on each side of the table?
We expect youngsters to be able to demonstrate
· an ability to collect, organize and display simple data sets
Make a presentation of all the kinds of pets owned by the students in your class. Include their weights, ages, and length from nose to tip of tail (where appropriate).
In Appendix A, the interested reader can see how these expectations of elementary school mathematical competence relates to the earlier discussion of the structure of the subject of mathematics as a whole.
The traditional mathematics curriculum at the elementary levels concentrates on the acquisition of computational skills, specifically getting students to master with some degree of automaticity the algorithms for adding, subtracting, multiplying and dividing whole numbers, fractions, and decimals. We believe it is time to think carefully about that enterprise.
We live in an age when a simple four-function calculator can be bought for less than the cost of a weekly newsmagazine. With the exception of the elementary grades of the schools of our country, almost all the calculation done in the country is done electronically. Thus the schools, in preparing students to calculate “by hand” are not preparing our students for the world they will encounter.
The counter-argument is often made that students need to understand the conceptual underpinnings of the computations that are done in the world around them. Indeed they do! We claim that such conceptual understanding does not flow from mindless repetition of un-understood mathematical ceremonies, but rather from a direct addressing of the conceptual issues involved in computation with whole numbers, fractions and decimals. Thus, at the youngest levels, the reader will find that we have stressed the importance of the order properties of numbers and estimation much more than is normally done in the traditional curriculum. At more advanced levels there are other interesting and subtle conceptual issues about numbers, the differences between the way in which they have been traditionally treated, and the way in which they are treated electronically.
Repetitive computational exercises are often performed without understanding. For example, how many educated adults understand why the procedures for long division or for multiplication and division of fractions work? Filling school and homework time with tiresome computational drill
· does not prepare students for the kinds of applications of mathematics that they are likely to encounter
· deadens the students’ interest and curiosity about mathematics
· uses up time that might better be spent in helping students develop a conceptual understanding of, and appreciation for, the subject of mathematics
Accordingly, we would be well advised to reconsider what we think is important mathematics in the elementary grades.
By the end of secondary school we ought to have a much more reasonable set of expectations of the mathematical capabilities of our students than we now do. In particular, there is a set of expectations we ought to have of students going directly into the world of work as well as of students going on to further education in subjects that are not mathematically demanding. We expect any school-leaving young adult, no matter what their formal mathematical training at secondary level, to be able to meet these expectations.
In our analyses of this question we have relied heavily on the work of some of our secondary school teacher colleagues who regularly bring “blue-collar” people from their community into their algebra classes to talk with students about the mathematics they use in their work.
It is important to point out that our expectations of mathematical competence for this group of young people is not what is normally referred to as “basic skills,” a pastiche of rote-memorized computational procedures and formulae, but rather a much more conceptual set of understandings of how to use the fundamental mathematical content they have learned in the contexts they are likely to encounter.
We have another set of expectations for students going on to further education in the natural sciences and engineering, the social sciences, and business and economics. These expectations are not very different either rhetorically or in content from those put forward by the National Council of Teachers of Mathematics in their Curriculum and Evaluation Standards for School Mathematics. They do differ, however, in what we regard as an important way, i.e., their organization of the mathematics by object ´ action.
In this section we have outlined these two sets of expectations as school-leaving standard and advanced.
By the end of Grade 12 we expect students to be comfortable with the numerical computations at least conceptually and to be able to measure lengths, areas, volumes, weights and time. Minimally, we expect all students to be able to reason qualitatively about the order properties of integers, fractions and decimals as well as be able to estimate length, weight, area, volume, time and number of things in their surround. We also expect students to be able to perform approximate numerical computations readily.
We expect some students to be able to undertake number-theoretic tasks, as well as intricate estimates of number, length, area, volume, weight and time that they encounter in their surround.
We expect all students to be able to scale lengths and read and interpret visual representations such as blueprints, maps, floor plans and clothing patterns.
We expect some students to be able to scale areas and volumes as well as to be familiar with geometrical concepts and constructs, and to be able to formulate, manipulate, and interpret geometrical models of situations in the world around them.
We expect all students to be able to evaluate algebraic expressions, to solve simple equations and inequalities, and to be able to read and interpret graphs. We also expect students to be able to model simple dependencies qualitatively and to sketch qualitative graphs of those dependencies.
We expect some students to be able to formulate and manipulate quantitative algebraic models of the world around them using symbolic, numerical and graphical representations, and to be able to reason, at least qualitatively, about both rates of change and accumulations of functions.
We expect all students to understand the consequences of the law of large numbers, elementary statistical analysis, and the use of statistical evidence in the communications media.
We expect some students to be comfortable with the concepts of statistical independence, conditional probability, and exploratory data analysis.
We expect all students to be able to generate and enumerate simple permutations and combinations.
We expect some students to be comfortable with iterative and recursive algorithms, discrete modeling, and optimization.
As a society and as educators, we assess both performance and competence in education in a variety of ways and for a variety of purposes. Broadly speaking the purposes are
serving instruction
accountability
selection
licensure
Assessing student performance in order to inform instruction is something that all teachers do. It is often the case that an external agency of some sort gets involved in assessment, nominally to serve instruction. The time lapse between the administration of the tests and the reporting of “scores” to teachers who might be able to use the information is such that there is little reason to assume that any such testing by an external agency has much to contribute to assessment for instruction.
Assessing for the purpose of saying how well a student, or a class, or a school, or an instructional program is doing is the primary purpose of assessment for accountability. Traditionally such information has been presented in one of two quite different forms, norm-referenced and criterion-referenced. Norm-referenced accountability statements involve comparing students’ performance (or classes or schools) to one another and then presenting the results of those comparisons in rank order. It should be noted that this can only be done if the performance of the students can be encoded in a unidimensional measure.Criterion-referenced accountability statements involve comparing students’ performance (or classes or schools) to some predetermined set of performance criteria without regard to how they compare to one another. It should be noted that this can only be done if one has a clearly defined set of performance criteria that reflect one’s theory of competence in the domain being assessed.
Assessing for selection is normally done for the purpose of helping to ascertain whether a student will have access to limited resources. Such assessment is often employed in order to inform decisions about access to select universities, programs for gifted music students, special education programs, etc.
Assessing for the purposes of licensure is normally done in order to ascertain whether the people being assessed have exceeded some threshold of minimal competence and are thus permitted to practice in an unsupervised fashion the skill that they have demonstrated. Such skills include driving automobiles, swimming in the deep part of the pool, barbering, butchering, working as an electrician or a plumber, etc.
Although it has never clearly articulated its stance with respect to these purposes, the Balanced Assessment project has focused it attention primarily on assessment to serve instruction and assessment for accountability, largely through the mechanism of assessing the performance of students on collections of tasks that the BA sites devised or adapted.
In 1992 the National Council of Teachers of mathematics undertook the development of a report on assessment to complement its earlier Curriculum and Evaluation Standards for School Mathematics. At the end of this document is a table summarizing the shifts in assessment practice that the NCTM is calling for. We cite that table here.
Major Shifts in Assessment Practice
|
toward |
away from |
|
assessing students’ full mathematical power |
assessing only students’ knowledge of specific facts and isolated skills |
|
comparing students’ performance with established criteria |
comparing students’ performance with that of other students |
|
giving support to teachers and credence to their informed judgment |
designing “teacher-proof” assessment systems |
|
making the assessment process, public, participatory and dynamic |
making the assessment process secret, exclusive and fixed |
|
providing students multiple opportunities to demonstrate their full mathematical power |
restricting students to a single way for demonstrating mathematical knowledge |
|
developing a shared vision of what to assess and how to do it |
developing assessment by oneself |
|
using assessment results to ensure that all students have the opportunity to achieve their potential |
using assessment to filter and select students out of the opportunities to learn mathematics |
|
aligning assessment with curriculum and instruction |
treating assessment as independent of curriculum or instruction |
|
basing inferences on multiple sources of evidence |
basing inferences on restricted or single sources of evidence |
|
viewing students as active participants in the assessment process |
viewing students as the objects of assessment |
|
regarding assessment as continual and recursive |
regarding assessment as sporadic and conclusive
|
|
holding all concerned with mathematics learning accountable for assessment results |
holding only a few accountable for assessment results |
This summary of the past and desired future of assessment in mathematics is as clear a set of guidelines as one could ask for in designing mathematics assessment. However, there is little, if anything, in this summary that could not have been written, with appropriate changes of adjective, by a task force of the National Council of Teachers of English. The central problem of changing the nature of assessment in mathematics must be faced in the design of actual mathematics assessments that reflect these guidelines. Roughly speaking, that is what the Balanced Assessment in Mathematics Project is about.
Balanced Assessment in Mathematics (BA) is a National Science Foundation project charged with developing new approaches to the assessment of mathematical competence in the elementary and secondary grades. The project is being carried out at four sites: the University of California at Berkeley, Michigan State University, the Shell Mathematics Centre of the University of Nottingham and the Educational Technology Center of the Harvard University Graduate School of Education. Support for the Berkeley and Nottingham sites of the project began in July of 1992; support for the Michigan State and Harvard sites began in the fall of 1993.
The main goal of Balanced Assessment is to produce assessment that can be used in classrooms throughout the nation — assessments that reflect the values of the mathematics reform movement as articulated in the National Council of Teachers of Mathematics Curriculum and Evaluation Standards. The assessments created by Balanced Assessment are designed to provide students, teachers, schools and parents with useful information about how students and programs are doing with respect to those standards.
By the end of 1995, BA will have completed the piloting of packages of assessment at each of three levels, elementary, middle school, and high school. The packages have assessment tasks and suggestions for longer projects to be done throughout the school year. Teachers and students use a package to create a set of selected works for each student which can be scored and used to document that student’s mathematical achievement, as well as to provide a balanced picture of that student as a learner of mathematics.
The type of assessments that BA is creating contrast sharply with traditional forms of testing, which rely primarily on multiple-choice questions. On standardized tests students are expected to answer each item in a minute or two. Such tests make no claim to assess a student’s problem-solving abilities, nor do these test provide information about how a student reasons, communicates mathematically or makes connections across mathematical content.
BA’s focus is on rich, mathematically complex work that requires students to create a plan, make a decision or solve a problem — and then justify their thinking. The contents of each assessment package range from short tasks to extended investigations and projects involving a week or more of work, and which include evidence of student collaboration, reflection and growth.
Further the project believes that assessment that is worthwhile to teachers, students, and others with a valid interest in what students can do mathematically, must also have the following characteristics:
· Assessment focuses on important, grade-level appropriate mathematics. Since assessment can only sample from all that is learned, it must sample as effectively as possible — by concentrating on the most important and useful mathematics taught and learned at that grade level, as defined by the NCTM Standards.
· Assessments are worthwhile learning activities — not digressions from learning. For the student, assessment is a tool that helps further the understanding of important mathematical ideas. For the teacher, assessment is student work that informs and augments instruction. Worthwhile assessment is not something students and teachers “stop and do,” but a way to further what they are already doing.
· The assessment maintains a focus on accessibility and equity for all students. The student must have — and the teacher and student must perceive that the student has — a fair opportunity to do his or her best. Assessments are designed to provide a student of either gender and of any cultural, linguistic and socio-economic background with the means to do his or her strongest mathematical work.
· Assessment elicits scorable, informative student work. The assessments are designed to elicit more than just an answer from the student. Rather, students are asked to solve a problem, show their thinking, create a product. The information in the student’s response, and the features of the student’s work that are evaluated, give a picture of his or her understanding of mathematical concepts, strategies, tools and procedures.
Clearly, the stated intent of the Balanced Assessment in Mathematics Project is entirely consonant with the directions in which the NCTM would like to see assessment in mathematics move. More to the point, the products of its efforts are also consonant with these directions and, in our view, represent a major step forward.
While there are no differences between the members of the Harvard Group and the BA project as a whole with respect to overall strategic goals, there are several areas in which the work of the Harvard group of BA differs from that of the other project sites. These include
task design and new task types
“weighting” of tasks
writing rubrics for tasks
scoring students performance
balancing assessment packets
The Harvard Group went about the process of task design in a way that differed from the other groups and was largely informed by the object ´ action analysis of the domain that it had made at the outset. This led to a particular kind of analysis of task demands, and a particular strategy for writing scoring rubrics for tasks. It also led to an explicit procedure for the balancing of tasks.
In addition to these procedural differences, there are two philosophical differences:
1. We believe that human performance in any cognitive domain of interest, including mathematics, is too complex to be reduced to unidimensional measures. Scoring performance of students should reflect this complexity. In keeping with this position, we do not accept the idea giving a student a single score on a task.
In addition to the trivialization of complexity that accompanies unidimensional measures, the use of such measures opens the door to a great deal of social mischief by making it easier to compare students to one another rather than to established criteria as called for by the NCTM and others.
2. Also in keeping with the NCTM Assessment Standards, we believe in making assessment public rather than secret. Well-crafted tasks aimed toward assessing well-defined skills and understandings need not be kept secret, either before or after they are administered. Indeed, if one wishes, as the draft NCTM Assessment Standards call for, to have assessment “...aligned with curriculum and instruction” and to be understood as “...continual and recursive” and for the community of mathematics educators and the public to have a “...shared vision of what to assess and how to do it,” then keeping the tasks secret is counterproductive.
We turn now to a detailed description of some of the ways the Harvard Group of the Balanced Assessment Project has gone about doing its work for the past two years.
For most of the period of the grant the primary responsibility of each of the sites of the BA project was to design assessment tasks, to try them in both classroom and clinical settings, and to revise them in the light of student reaction to those trials. The BA project undertook to design three quite different sorts of tasks. They are
skills tasks tasks that primarily test the ability to manipulate and compute
problems tasks that primarily test the ability to model, infer, and generalize
projects tasks that test the ability to analyze, organize, and manage complexity
The Harvard Group of BA approached the problem of Task Design within the framework of the Mathematical Content Matrix presented earlier in this document. First we decided what mathematical objects and actions we expect students to have mastered; this gave us a reasonably focused view of the mathematical playing fields within which we needed to design tasks.
If one needs to generate a large number of assessment tasks, it is clear that thinking in terms of task types, rather than in terms of individual tasks, is a useful strategy. Wherever possible we strove to make clusters of tasks that were linked by context, or mathematical structure, or both. By way of illustrating this strategy as well as demonstrating what we mean by each of the three categories of task, here is an example of each.
Here is a diagram of a new kind of race track. What is the total length of the track?
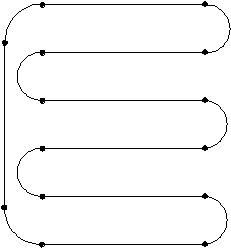
The combined length of all the curved sections is 100 meters.
The length of each straight section is 100 meters.
Two joggers set out at the same time and from the same place and in the same direction to jog on a circular track. Jogger A jogs at a constant speed which is exactly twice the speed of jogger B. They jog for the same period of time and stop after A has completed 6 laps around the track. (You may ignore the time it takes for the joggers to get up to speed at the outset and to slow down at the end.)
An observer at the geometric center of the track monitors the angle between the two joggers as a function of time. Sketch a graph of this observer’s data.
How would the graph of the observer’s data differ if the two runners had started off in opposite directions at the outset?
Track of Dreams
The Situation
In the last twenty years, science has improved the conditions of competition in many sports. Some things, however, have not changed in ages. The dimensions of playing fields and courts in team sports, tennis and some other court sports have remained the same, largely to preserve the tradition of the sport. However, in track and field these unchanged dimensions are primarily due to the fact that the track and other venues are often associated with football or soccer fields and, therefore, must rely on their dimensions. If an average football field is about 140 by 65 yards, it allows for a track oval around it with the length of the inside lane of about 400 meters. A soccer field, which is shorter but wider, produces roughly the same length of the track.
For international competition, 400 meters is the standard length of the inside lane on the track. In addition, the following conditions are required for international competition
· The width of the each lane must accommodate the runners in such a way that two runners running side by side in adjacent lanes would not interfere with each other.
· The track must have 8 lanes.
· The 100 meter race must be run along a straight path.
· The finish line must be at the end of a straight part of the track, continuous across all lanes and perpendicular to the track.
· The starting line must also be perpendicular to the track, but need not be in the same place for all lanes (this is a “staggered” start necessitated by the different lengths of the lanes).
There are also restrictions about the type and quality of the surface and some other conditions necessary for accreditation, but these are not important here.
The Problem
You have been hired by the Santa Monica Track Club (the most prestigious in the country) to design a new track. Your job is to analyze a number of possible shapes and present the club with three alternative shapes for the new track and to also present arguments — pro and con — for each of these. The track is to be built solely for the track-and-field purposes so there will be no external constraints with respect to the dimensions or directions of the track.
Some of the international rules are a matter of tradition and could be relaxed for a new scientifically designed track. However, all the conditions listed above (except for the length of the inside lane) must be met. Furthermore, there are other physical and esthetic constraints that further limit the design possibilities:
· The track must accommodate races for 100, 200, 400, 800, 1500, 3000, 5000 and 10000 meters. Some other races, such as 1 mile or 50 meters, may be run there as well, but are not a priority, so they should not figure in the computations.
· The length of the shortest lane of the new track must be some multiple of 100 meters in length.
· For construction reasons, all parts of the track must be designed as parts of circles or straight lines; at the transition points from one part to another, these circles and lines must be tangent to each other.
· The lanes cannot separate at any point, that is, crossing the track at any point in the direction perpendicular to it must cut across all eight lanes in succession with no space between them.
·
The faster you run the harder it is to turn, so races from 50 to
400 meters must be run in such a way that no one makes sharp turns; for longer
races the turns could be made tighter; overall, no part of the course for a
specific race can contain a part of a circle with a diameter (measured in
meters) smaller than ![]() where 9,000 is a constant measured in
square meters which was derived by observation. This constraint is designed to
prevent runners from falling on turns or one runner having an advantage over
another.
where 9,000 is a constant measured in
square meters which was derived by observation. This constraint is designed to
prevent runners from falling on turns or one runner having an advantage over
another.
· An attempt must be made to minimize the overall dimensions of the track, for two reasons: Costs should be considered, although a superior track might be chosen despite its higher price. Spectators should be seated so as to allow them to see as much of the race as possible; for this reason a straight track would be out of the question.
1. Several designs have already been submitted by different parties. As the official design consultant you must sift through these and explain why some of them must be rejected. Even though you reject some or all of these, they may give you ideas about possible designs. Write a letter to your assistant, explaining which of these proposals are rejected and why, and point out some possible modifications which could make similar designs acceptable. (In all instances the distances are approximate and measured along the track between the marked points.)
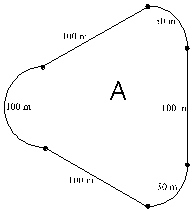
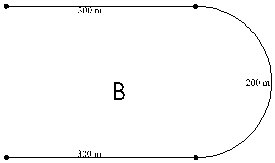
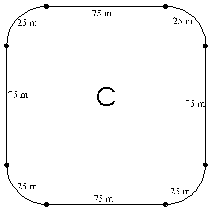

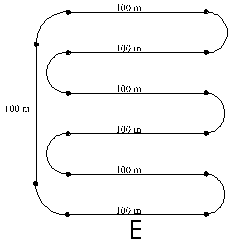
The combined length of all the curved pieces is 100 meters.
2. Suppose now that you are the assistant who received the above letter. You must respond to the letter with proposed modifications of these designs. Note that in proposal E the combined length of all the curved parts could not only be 100 meters, but also 200, 300 meters or some other multiple of 100 meters. In your response, you will need to analyze several possible variations, including changing the length in the case of design E. Write such a letter with detailed mathematical analysis.
3. Most of the tracks under consideration have the unfortunate property that they require a staggered start. This happens because the lanes are not all of equal length and the athletes on the inside lanes are required to make a sharper turn than the athletes on the outside. Can you generate some possible designs that would satisfy all the conditions and would not require a staggered start for at least some of the races?
4. Having returned to your supervisory capacity, now is the time to find other possible shapes and write the final report on the proposal. If you believe that some of the conditions should be relaxed in favor of a specific design, you will need to convince a committee composed of athletes, administrators, architects and mathematicians. Therefore, your arguments must be clear, succinct and precise.
This third category of task, projects, deserves special comment because of the growing interest in the use of portfolio assessment. We found that many users of portfolio assessment took the position that the essential feature of such assessment was the fact that the student chose, with or without guidance from the teacher, what pieces of work to include in his or her portfolio. While this in itself is desirable, it can lead to portfolio content that is minimally demanding and hardly able to exhibit the student’s strengths and weaknesses. The situation may be compared to that of a student who applies for admission to a music conservatory and submits a tape of playing scales.
Harvard’s Balanced Assessment team thinks of projects as intellectual undertakings that require students to make an effort over an extended period of time to structure and formulate a problem, and then to analyze the problem as they have formulated it. Projects are not problems with unique, correct solutions. Projects are not long and complicated versions of problems that one normally assigns in the context of a classroom assignment. Projects are not problems that require tricky insights or inventions to solve. The essence of a Balanced Assessment project is that it is a task that requires a student to ruminate and reflect about a rich web of complexity, and to sort out some main threads that can serve as the basis for structuring a response.
In the course of addressing the problem that forms the core of the project as they have formulated it, students will have to perform a wide range of traditionally taught mathematical actions that might include manipulating algebraic symbols, plotting graphs, geometric constructions, compiling tables, and performing numerical computations. The accurate performance of these actions, as important as they are, is only a part of doing a Balanced Assessment project. Students are also asked to make inferences, draw conclusions, and present their work in both written and oral form.
In this section we describe some considerations that teachers should keep in mind as their students work on projects and as they, the teachers, assess the products of their students’ efforts.
Mathematics has traditionally been a subject in which we have insisted that students work alone. Whatever the merits of that viewpoint might be with respect to covering the content of the syllabus, it seems to us that project work is different. The essential issue in project work is development of desirable “habits of mind” about organizing and analyzing complexity. Adults, when confronted with tasks of this sort, often address them in groups. The reason for doing so is the intellectual resonance and symbiosis that leads groups of people to fashion far better solutions to complex problems when they work cooperatively than when they work in isolation. We suggest, therefore, that students undertake project work in small groups. You may want to give some thought to how groups ought to be composed and whether or not to juggle the composition of the small groups at various times during the school year.
This will vary with individual teachers. Some teachers will try to build a whole year’s work around projects. We find that it is often difficult to do this — there is always the nagging feeling that the curriculum is not being “covered.” On the other hand we feel that the kind of intellectual development that coping with a project offers is of sufficient importance that students ought to spend no less than 10% of their time, and probably as much as 25% of their time on such work.
One could imagine students spending one quarter of their time every week throughout the school year on their continuing project work. Alternatively, one can imagine intensive two week project periods distributed throughout the year. During these periods students would use all of their mathematics time for project work. Other time arrangements are also possible. Ultimately, it will be individual teachers who make this decision in light of their understanding of what best fits the needs of their classes.
We think that project work should be presented both in writing and orally. The written presentation should describe the contextual setting and how, within that setting, the problem is defined. The written presentation should present explicit arguments for why the projects omits consideration of some factors and includes others. It should show clearly how solution was approached. It should indicate clearly where there are further issues to investigate.
The oral presentation should be made publicly to the entire class after the teacher and at least some of the students have read the written presentation. Following a brief outlining of the written document, the presenting students should entertain questions and comments.
Here is one possible specific way you might organize the presenting of project work. Have each group submit a written report of its work. In addition, ask each group to read the written reports of two other groups. On the day of the oral presentations, have each group present its work — and then serve as a panel to answer questions put to them by the other groups that have read their work, as well as by the teacher and other students.
All Balanced Assessment projects ask the student to prepare a document with an intended purpose for an intended audience. Consequently, scoring of projects comes down to an analysis of two questions:
Is the document suitable for the specified audience?
Does the document fulfill the requested purpose?
To aid in evaluating student project work in the light of these two criteria, we suggest the following six perspectives; each perspective may allow you to reach conclusions about some aspect of the student’s effort.
Organizing the Subject: How well does the student structure a large collection of interrelated issues and identify possible problematic areas? Are the constraints described in the problem made clear at the outset? How well does the student argue the relative importance of factors that are taken into consideration in addressing the problem, and the relative unimportance of factors that are ignored? Does the report proceed in a logical manner?
Analyzing the Problem: How well does the student define the problem? Is the student clear about all the resources, both tools and information, that will be needed to address the problem? Does the student draw appropriate implications about the given data?
Accuracy and Appropriateness of Computation/Manipulation: Are the symbolic manipulations carried out accurately? Are the graphs plotted correctly? Are the axes labeled sensibly? Is the scale reasonable? Are the geometric constructions “constructable”? Are the table columns properly labeled? Are the computations that underlie computed columns clearly defined? Are the numerical computations done accurately? Are the graphs, charts, tables used appropriately? Are they pertinent to and do they strengthen the argument?
Thoroughness of Inquiry: Is the work perfunctory or thorough? Is the reader left to fill in many missing steps? Are all the implications of the complexity of the problem followed up and examined? Is the reporting level of detail adequate?
Clarity of Communication: Can the student’s work be read by a colleague who is previously unacquainted with the work? Is the student’s written presentation intelligible to another teacher? to the principal? to a group of parents?
Drawing Conclusions: o students draw reasonable conclusions from their work? Do they clearly explore the ways in which their work answers the questions they have posed?
Extending the Inquiry: Has the student identified interesting aspects of the problem that lend themselves to further exploration? Has the student noted related problems that might be approached in similar ways?
Finally, it should be said that we are mindful that teachers’ constraints and opportunities vary from place to place. Not everything we suggest will be desirable, or even possible, at every location. However, we are certain that challenging the students with a significant amount of project work will be rewarding and engaging to both teacher and student.
One of the strategies the Harvard Group of BA employed in order to design tasks that are fresh and engaging to student is to try to find new task types that students may not have encountered before. There are several such types that we found and/or developed. For the most part these are tasks that do not have unique correct answers. They are tasks that promote discussion, and occasionally debate, among students. We believe these to be important features of successful tasks.
The purpose of these tasks is to see how well students can mathematize a relationship that they are aware of perceptually but probably have never attempted to describe in any formal, not to mention quantitative, fashion.
Each of these tasks requires students to identify and describe formally a geometric property of some two or three dimensional shape. It is important to stress that properties such as “squareness” or “bumpyness” are not formal geometric properties. There are no formally correct and universally accepted answers to these questions. On the other hand, there are sensible (and non-sensible) answers.
For the sake of specificity, the following is an example.
Below is a collection of rectangles.
1. Which of the rectangles is the “squarest”?
2. Arrange the rectangles in order of “square-ness” from most to least square.
3. Devise a measure of “square-ness,” expressed algebraically, that allows you to order any collection of rectangles in order of “squareness.”
4. Devise a second measure of “square-ness” and discuss the advantages and disadvantages of each of your measures.

The elements of performance on these tasks are as follows:
a. choosing the most and least square, sharp, etc. figure
b. a verbal description of the geometric property being modeled
c. identifying the geometric elements that combine to form the measure
d. forming an algebraic relationship among these elements
e. computing values of the measure for various figures
f. discussing the advantages and disadvantages of the measure
The weight that should be assigned to the successful completion of these elements of the task increases as one goes down the list. In our view successful completion involves satisfactory completion of at least parts a through d.
Problems of this sort have several important virtues. Even very weak students can get started on them. At the same time, they provide an opportunity for strong students to display a great deal of sophistication. In addition, they exercise several quite important mathematical muscles that are rarely called upon in school mathematics. We refer here to the need for defining quantitative constructs — a central feature of the application of mathematics to both the natural and social sciences.
Appendix B contains a discussion of some of the directions one might go with the “square-ness” problem.
Another type of problem that we have introduced is known in some circles as “Fermi problems.” These problems ask for the estimation of quantities such as number, length, area, volume, weight, and time. Many of these quantities are measures of things that you are likely to encounter in everyday life, although they may not be quite in the form that you normally think of them.
These problems are called “Fermi problems” after Enrico Fermi, one of the great physicists of the twentieth century. Fermi taught for many years at University of Chicago where he used to ask his beginning graduate students “...to estimate the number of piano tuners in Chicago.”
In order to make the kinds of estimates that respond to Fermi problems, one must often make use of information that is not contained in the statement of the problem. Sometimes the necessary information will be the sort of thing you might already know. Sometimes you may have to use reference materials in order to find the necessary pieces of information.
Lets explore some ways of thinking about this sort of problem. Suppose we are asked “How many words in all the books in the school library?” How could we go about estimating this number?
If we knew
the number of shelves of books in library, and
the average number of books on a shelf, and
the average number of pages in a book, and
the average number of words on a page
then we could estimate the number of words. Suppose a school library has
600 shelves
and that on the average there are
16 books on each shelf
Suppose further, that there are, on the average,
250 pages in each book, and
400 words on each page.
We can estimate the number of words by multiplying
![]()
The size of this product is 960,000,000 words. How good is this answer? How well does it apply to your school library?
People are not accustomed to seeing problems in mathematics that do not have exactly one correct answer. How, then, are they to think about these problems? In particular, when is the answer to such a problem good enough? A rough guide is the following:
Devise two different strategies for arriving at an estimate of the desired quantity. If the larger of the two estimates is no more than 10 times the smaller estimate then there is a strong likelihood that the estimate(s) you have made is (are) reasonable.
For example, consider the illustrative problem that we worked on before, i.e. the number of words in all the books in the school library. Suppose we had approached the problem differently. Suppose we said that the library, on the average, buys 50 books a month during each of the 10 months of the school year. Suppose, further, that the library has been doing this for the 20 years that the school has been in existence.
We can now compute the number of words in all the books in the library in a quite different way.
![]()
This computation produces an estimate of 1,000,000,000 words.
Here are three quite different ways of arriving at an estimate the total distance a person walks in a day. One estimate attempts to take account of the total waking time of a person during the day, assumes that they are moving about a certain fraction of that time and that when they move, they do so at an assumed average speed.
Another estimate relies on the information that comes from a shoemaker who says that a pair of sneakers wear out after some number of miles. If you know how often you replace your sneakers then you can calculate an average distance walked (or run) in a day.
Finally, a third method of estimating the total distance a person walks in a day relies on following the person about and simply adding up the estimated distances they walk, including to and from school, store, ball field, around the house and school, and so on.
To be sure these estimates may not all yield the same number. Although they differ from one another, they are all reasonable ways of approaching the problem. If you estimate the distance a person walks by each of these three methods and they turn out to give numbers that are not very different from one another you may assume that you have made a reasonable estimate.
An effective way of probing a student’s understanding of the application of a concept in context is to ask the student to generate an example of the application of that concept. Typically, such questions do not have unique answers. For example, one might ask a student to give an example of a number that is an integer power of both 2 and 4, or an even function of x that is not constant but never exceeds 1 in absolute value.
This type of problem, i.e., of providing examples of a mathematical object that has a specified set of properties, is in our view underutilized in the assessment of mathematical competence. Here are some examples.
Give three examples of numbers that are evenly
divisible by 2, 3, 4, and 5.
Write a number whose value is between 1/4
and 1/5.
Draw a 4-sided figure with two pairs of sides of
equal length that is not a parallelogram.
Draw a triangle whose circumscribing circle’s center lies outside the triangle.
For each of the following pairs of functions, write a function which is everywhere at least as large as the smaller and no larger than the larger of the two functions
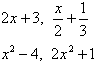
Design a red and blue painted dart board such that the chance of landing on red is three times the chance of landing on blue.
Devise two different techniques for alphabetizing a large list of names, for example all the students in your school. Contrast the efficiency of your techniques with one another.
In order to approach the problem of designing balanced assessment packages in mathematics one must have a clear view of the kinds of understandings and skills that we wish to assess in our students and the ways in which the tasks we design elicit demonstrable evidence of those skills and understandings. In what follows we shall describe how our view of the subject of mathematics, its objects and its actions, informs the design of tasks and the balancing of assessment packages.
Each task is classified according to domain, i.e. the mathematical objects that are prominent in the accomplishment of the task. Most of our tasks deal predominantly with a single sort of mathematical object although some deal with two. Each task offers students an opportunity to demonstrate a variety of kinds of skill and understanding.
In order to score student performance on a task one has to first analyze the task and decide on the nature of the demands that the task makes on the student. We considered the following four kinds of skill and understanding.
Modeling/Formulating: How well does the student take the presenting statement and formulate the mathematical problem to be solved? Some tasks make minimal demands along these lines. For example, a problem that asks students to calculate the length of the hypotenuse of a right triangle given the lengths of the two legs does not make serious demands along these lines. On the other hand, the problem of how many 3 inch diameter tennis balls can fit in a (rectangular parallelepiped) box that is 3" ´ 4" ´ 10", while exercising the same Pythagorean muscles in the solution, is rather different in the demands it makes on students’ ability to formulate problems.
Transforming/Manipulating: How well does the student manipulate the mathematical formalism in which the problem is expressed? This may mean dividing one fraction by another, making a geometric construction, solving an equation or inequality, plotting graphs, or finding the derivative of a function. Most tasks will make some demands along these lines. Indeed most traditional mathematics assessment consists of problems whose demands are primarily of this sort.
Inferring/Drawing Conclusions: How well does the student apply the results of his or her manipulation of the formalism to the problem situation that spawned the problem? Traditional assessments often pose problems that make little demand of this sort. For example, students may well be asked to demonstrate that they can multiply the polynomials (x+1) and (x–1) but not be expected to notice (or understand) that the numbers one cell away from the main diagonal of a multiplication table always differ from perfect squares by exactly 1.
Communicating: How well do students communicate to others what they have done in formulating the problem, manipulating the formalism, and drawing conclusions about the implications of their results?
Since we do not expect each task to make the same kinds of demands on students in each of the four skills/understandings area, we assign a single digit measure of the prominence of that skill/understanding in the problem according to the following scale of weighting codes:
Weighting codes
0 not present at all
1 present in small measure
2 present in moderate measure, and affects solution
3 a prominent presence
4 a dominant presence
Note that these numbers are not measures of student performance but measures of the demands of the task for a given performance action.
Most tasks will involve these skills and understandings in some combination. Needless to say, different tasks will call differently on these actions. Therefore, it is necessary in designing tasks to pay particular attention to the nature of the demands on performance that the tasks make.
What does all of this mean for the fashioning of both tasks and balanced assessment packages?
For each task one decides on the basis of experience, taste and judgment, ideology and philosophy, how the task’s demands should be distributed among the content domains:
Content domain weighting
|
Number and Quantity |
|
|
Shape and Space |
|
|
Pattern and Function |
|
|
Chance and Data |
|
|
Arrangement |
|
[Entries must sum to 1.]
and among the various sorts of performance actions:
Process weighting
|
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
|
|
|
|
[Each entry is on a 0-4 scale.]
This is precisely how we went about the design of our assessment packages. Each of the tasks we designed was weighted in this fashion. Balanced packets of assessments at different grade levels were then assembled by suitably assembling tasks into collections whose aggregated weights reflect our thoughts about appropriate demands for that grade level.
At the youngest grades we placed great emphasis on Number and Quantity and Shape and Space objects. We tried to stress the Modeling/Formulating and Inferring/Drawing Conclusions actions much more than do traditional assessment programs that tend to concentrate on assessing students’ ability to manipulate number and shapes. In addition, we tried to devise fresh and interesting ways of having students communicate with one another as well as report to us on their efforts.
At the other end of the grade spectrum, the distribution of emphasis shifted. The Number and Quantity and Shape and Space objects are still present but the Chance and Data and Arrangement objects are now a significant portion of the assessment, and the Pattern and Function object assumes great importance. The demands on students are more subtle and nuanced. Apart from technical questions designed to ensure that transforming and manipulating skill exceeds some reasonable threshold, strong emphasis is placed on tasks that make extensive Modeling/Formulating and Inferring/Drawing Conclusions demands. Here too we have attempted to devise a wide variety of ways for students to communicate with one another and with us about their efforts.
The particular distribution of emphasis for each of the packages we designed is discussed in the introduction to that package.
After a task has weights assigned that reflect the different demands the task makes on a student it is possible to write scoring rubrics. Here for example is a task appropriate to secondary level, along with the weighting of the task and the scoring rubric written for it. The rubric is specific to the task and analyzed along the lines of the performance actions we have defined.
No one can write rubrics that exhaustively anticipate the richness and variety of student responses. Teachers who use the rubrics we write are urged to use them as a guide where they are helpful, and to use their own good judgment when they find our rubrics not shedding light on their students’ efforts.

1. An empty fruit crate weighs 5 pounds. When filled with 10 melons it weighs 35 pounds. Plot the weight of the fruit crate as a function of the number of melons it contains.
2. An empty 10 gallon
can weighs 5 pounds. When filled with melon juice it weighs 35 pounds.
Plot the weight of the can and juice as a function of the volume of
melon juice in the can.
3. Discuss the similarities and differences of your two graphs.

Melons and Melon Juice L016 scoring rubric
Math Domain
|
|
|
Number/Quantity |
|
Shape/Space |
Pattern/Function |
|
|
|
|
|
|
|
|
|
|
|
|
Chance/Data |
|
Arrangement |
|
|
Math Actions (possible weights: 0 through 4)
|
|
3 |
Modeling/Formulating |
2 |
Manipulating/Transforming |
|
|
|
|
|
|
|
|
2 |
Inferring/Drawing Conclusions |
2 |
Communicating |
Math Big Ideas
|
|
|
Scale |
|
Reference Frame |
Representation |
|
|
|
|
|
|
|
|
|
|
|
Continuity |
|
Boundedness |
|
Invariance/Symmetry |
|
|
|
|
|
|
|
|
|
|
|
|
Equivalence |
|
General/Particular |
|
Contradiction |
|
|
|
|
|
|
|
|
|
|
|
Use of Limits |
|
Approximation |
|
Other |
|
|
|
|
|
|
|
|
The essential point in this problem is for students to display an understanding of the difference between a discrete linear function and a continuous linear function. Graphs for these functions are shown on the following page.
The two graphs are similar in the respect that they both begin at the point (0,5) and end at the point (10,35), with a constant rate of change.
The symbolic form of both of these functions is Weight = 5 + 3n.
The functions differ in the following respects:
In the case of the melons, the domain is the integers 0-10; in the case of the melon juice the domain is continuous between 0 and l0.
In the case of the melons, the range is the integers 5,8,11,14,17,20,23 26,29,32,35; in the case of the melon juice the range is continuous between 0 and 35 pounds.

|
|
partial level |
full level |
|
Modeling/ (weight: 3)
|
Set up a weight vs. object (melons or gallons of juice) graph. Give some evidence of linear dependence. |
Make a clear distinction between linear discrete and linear continuous dependence. |
|
Transforming/ (weight: 2)
|
Plot the linear functions with reasonable accuracy. |
Show the plotted functions with a clear distinction between the discrete and continuous dependence. |
|
Inferring/ (weight: 2)
|
Realize that both graphs have the same angle of upward trend.
|
Realize that both graphs start at (0,5), but that the range of the melon graph will be discrete values satisfying the equation W=5+3n. |
|
Communicating (weight: 2)
|
Provide only graphs with no prose description of similarities and differences. |
Give a prose description of each graph in detail, and present an argument for the graphs being similar or distinct. |
What does all this mean for the scoring of students who use balanced assessment packages? There are several premises that underlie our views on scoring. These are:
· The BA assessment packages are designed to allow their users to make informed judgments about both the success of individual students and the success of instructional programs as a whole.
· All BA tasks are inherently multidimensional and thus notions of unidimensional ranking of students, independent of purpose, are inappropriate.
· Scoring along any single dimension is at best ordinal and thus notions of ratio or even interval scales are inappropriate.
Each task is classified according to domain, i.e. the mathematical objects that are prominent in the accomplishment of the task. Most of our tasks deal predominantly with a single sort of mathematical object although some deal with two. Each task offers students an opportunity to demonstrate a variety of kinds of skill and understanding.
For each task we expect the person scoring the student’s performance to use one of the following performance icons for each of four different kinds of skill and understanding. These performance icons may be thought of as ordinal measures with roughly the following values:
![]() the student shows little evidence of
skill or understanding
the student shows little evidence of
skill or understanding
[internal code 0]
![]() the student shows a fragile
skill or understanding
the student shows a fragile
skill or understanding
[internal code 1]
![]() the student shows an adequate level
of skill or understanding
the student shows an adequate level
of skill or understanding
[internal code 2]
![]() the student shows a deep and robust
level of skill or understanding
the student shows a deep and robust
level of skill or understanding
[internal code 3]
Here is a copy of a sheet recording the performance of one student on the “Melons and Melon Juice” task.
Content domain weighting
|
Number and Quantity |
0 |
|
Shape and Space |
0 |
|
Pattern and Function |
1 |
|
Chance and Data |
0 |
|
Arrangement |
0 |
[Entries must sum to 1.]
Process weighting
|
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
3 |
2 |
2 |
2 |
[Each entry is on a 0-4 scale.]
Student performance
|
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
||||
|
score
|
wtd. score 6/9 |
score
|
wtd. score 4/6 |
score
|
wtd. score 2/6 |
score
|
wtd. score 4/6 |
Since realistically any single task is unlikely to involve more than two mathematical domains or kinds of mathematical object, the content domain weighting table is unlikely to have more than two rows with entries. Indeed, most tasks will have entries in only one row. The assessor enters into each of the pertinent cells one of the four performance icons (or their internal codes) described above.
In this instance the task is deemed to be primarily about function as the mathematical object; it makes prominent demands on a student’s ability to model, and moderate demands on the students ability to manipulate, infer and communicate. These demands are indicated by weights of 3, 2, 2, and 2 respectively in the process weighting table.
The student received high partial credit, i.e. ![]() or 2, for
Modeling/Formulating. Since the weight in this area is 3, the student
received a weighted score on Modeling/Formulating for 2 ´ 3 = 6 out of 9 possible points. Similarly, the student
received a weighted score of 2 ´ 2 = 4
out of 6 for Transforming/Manipulating. On Inferring/Drawing Conclusions, the
student received low partial credit, i.e.
or 2, for
Modeling/Formulating. Since the weight in this area is 3, the student
received a weighted score on Modeling/Formulating for 2 ´ 3 = 6 out of 9 possible points. Similarly, the student
received a weighted score of 2 ´ 2 = 4
out of 6 for Transforming/Manipulating. On Inferring/Drawing Conclusions, the
student received low partial credit, i.e. ![]() , for a weighted score of 1 ´ 2 = 2 out of 6. For Communicating, the
weighted score was
, for a weighted score of 1 ´ 2 = 2 out of 6. For Communicating, the
weighted score was
2 ´ 2 = 4 out of 6.
It is important to stress that the numbers used in computing weighted scores from raw scores all vanish in the final presentation of the student’s record.
Assessing the overall performance of individual students in mathematics requires us to record their performance on individual tasks and to aggregate their performance across a large number of individual tasks while preserving, to as large an extent as possible, the richness of the information yielded by the observations on individual tasks.
One could imagine reporting the complete student record of performance on each task. This volume of information is likely to overwhelm whoever looks at it, and, except in the case of the clinician specifically interested in as particular student, to be of little use to anyone. For example, a complete student record might have this structure.
Complete student record
|
student name |
class/date |
|
|
|
|
action task/domain |
Modeling/ Formulating |
Transforming/ Manipulating |
Inferring/Drawing |
Communicating |
|
task 1 |
|
|
|
|
|
Number and Quantity |
|
|
|
|
|
Shape and Space |
|
|
|
|
|
Pattern and Function |
|
|
|
|
|
Chance and Data |
|
|
|
|
|
Arrangement |
|
|
|
|
|
task 2 |
|
|
|
|
|
Number and Quantity |
|
|
|
|
|
Shape and Space |
|
|
|
|
|
Pattern and Function |
|
|
|
|
|
Chance and Data |
|
|
|
|
|
Arrangement |
|
|
|
|
|
etc. |
|
|
|
|
Each cell in this table contains the weighting code of that task on the skill/understanding in question for a given kind of mathematical object. Each cell corresponding to a task the student has tried also contains a performance icon (or its internal code) denoting the quality of his or her performance on that aspect of the task.
Such a body of information might well be useful to teachers for informing instructional decisions and, in addition, can be thought of as a cumulative record of a student’s mathematics activities throughout the school years. However, it may be somewhat inundating for purposes of accountability. For such purposes it becomes necessary to aggregate student performance over several, possibly many tasks. Let us consider a specific example.
Here is a comparison of the work of two students on a collection of tasks. The students were asked to choose five tasks. Their choices were to be governed by the following constraints:
no more than 2 tasks from any single content domain
no more than 3 skills tasks
at least 2 problems
Here are the results of the students’ efforts:
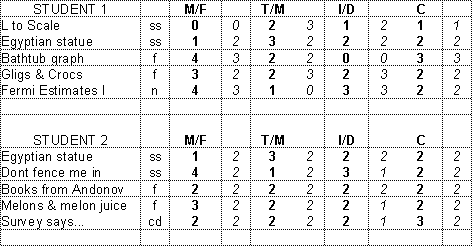
The leftmost column indicates the name of the task. The next column indicates the predominant mathematical content domain (n - Number and Quantity, ss- Shape and Space, f - Pattern and Function, cd - Chance and Data, a - Arrangement). The bold figures are the weights given to each of the mathematical action categories for each of the problems. The figures in italics are the scores (0, 1 or 2 for partial level, 3 for full level) that each student received on that section of each of the problems.
Note that a column sum of the scores at this stage would record the fact that the students were equally competent at modeling, transforming, and communicating, although a teacher might intuitively feel that there were distinctions to be made on the performance of these two students.
To calculate the weighted sum of the first student’s performance on modeling in the domain of Function we note that the first function problem was assigned an M/F weight of 4 and that the student made 3 marks (i.e. full level) on it. The second problem in the domain of function was assigned an M/F weight of 3 and the student made partial level on it, receiving 2 marks. Thus the student received 18 M/F marks (3´4 + 2´3) out of a possible 21 (3´4 + 3´3) in the domain of function, resulting in a decimal score of 0.86.
Similar calculations are done for each cell. Performance icons are then assigned as follows.
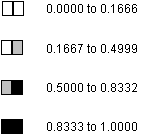
Here are the records of these two students aggregated over domains.
Student record aggregated over tasks within content domains
|
Student 1 |
|
|
|
|
|
action domain
|
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
Number and Quantity |
|
|
|
|
|
Shape and Space |
|
|
|
|
|
Pattern and Function |
|
|
|
|
|
Chance and Data |
|
|
|
|
|
Arrangement |
|
|
|
|
|
|
|
|
|
|
Student record aggregated over tasks within content domains
|
Student 2 |
|
|
|
|
|
action domain
|
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
Number and Quantity |
|
|
|
|
|
Shape and Space |
|
|
|
|
|
Pattern and Function |
|
|
|
|
|
Chance and Data |
|
|
|
|
|
Arrangement |
|
|
|
|
|
|
|
|
|
|
Note that this presentation clearly reflects the inherent difference in the performance of the two students, which the numerical presentation did not reveal.
It should be stressed that at this level of aggregation there are no longer any numerical measures entered in the cells of the aggregate student record, only the aggregated performance icon appropriate to that cell.
The full power of this method of recording and reporting student performance becomes clear when one has enough data to fill all the cells. Here are the student records of four fourth grade students aggregated over eleven tasks. These tasks were distributed over the content domains as follows: 4 Number and Quantity, 1 Shape and Space, 3 Pattern and Function, 1 Chance and Data and 2 Arrangement.
Student record aggregated over tasks within content domains
|
Student A |
|
|
|
|
|
action domain |
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
Number and Quantity |
|
|
|
|
|
Shape and Space |
|
|
|
|
|
Pattern and Function |
|
|
|
|
|
Chance and Data |
|
|
|
|
|
Arrangement |
|
|
|
|
|
|
|
|
|
|
Student record aggregated over tasks within content domains
|
Student B |
|
|
|
|
|
action domain |
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
Number and Quantity |
|
|
|
|
|
Shape and Space |
|
|
|
|
|
Pattern and Function |
|
|
|
|
|
Chance and Data |
|
|
|
|
|
Arrangement |
|
|
|
|
|
|
|
|
|
|
Student record aggregated over tasks within content domains
|
Student C |
|
|
|
|
|
action domain |
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
Number and Quantity |
|
|
|
|
|
Shape and Space |
|
|
|
|
|
Pattern and Function |
|
|
|
|
|
Chance and Data |
|
|
|
|
|
Arrangement |
|
|
|
|
|
|
|
|
|
|
Student record aggregated over tasks within content domains
|
Student D |
|
|
|
|
|
action domain |
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
Number and Quantity |
|
|
|
|
|
Shape and Space |
|
|
|
|
|
Pattern and Function |
|
|
|
|
|
Chance and Data |
|
|
|
|
|
Arrangement |
|
|
|
|
|
|
|
|
|
|
The reason for the use of the performance icons now becomes clear. It is possible for a teacher or parent to grasp quickly and perceptually how well a child is doing, and where his or her strengths and weaknesses lie. The pattern of light and dark distributed through a table is well known to be readily intelligible as a conveyer of a large body of data. Its most widespread use is to be found in Consumer Reports and other such publications.
Finally, it is often informative to aggregate these data across mathematical actions. In the case of our four students one obtains
Student record aggregated over tasks
|
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
|
|
|
|
Student record aggregated over tasks
|
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
|
|
|
|
Student record aggregated over tasks
|
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
|
|
|
|
Student record aggregated over tasks
|
Modeling/ |
Transforming/ |
Inferring/Drawing Conclusions |
Communicating |
|
|
|
|
|
Note that all of the students communicate reasonably well. Except for Student D, they are all weak in making inferences and drawing conclusions. Except for Student A, they are all reasonably able to do the kinds of manipulations that are traditionally expected of them in mathematics classes. Except for Student D, they do not model and mathematize very well.
From these aggregated data one might conclude that the mathematical strengths and weaknesses of Students B and C are similar, but looking at the unaggregated data for these students one might well come to the conclusion that they have different instructional needs.
We believe that further aggregation of student performance data does not make any sense. While it is possible to collapse these data further, we wish to stress as forcefully as we can that any such aggregation will substantially reduce the utility of these materials to contribute to informed decisions about students.
We now turn to the question of how diverse tasks are assembled into “balanced” assessment packets. The project undertook to build assessment that was balanced along a variety of dimensions which included content, task type, duration of task, etc. As of this writing (fall 1995), there is as yet no project-wide procedure for balancing packets. The Harvard Group has a devised a procedure for assembling and balancing packets which we describe here.
In order to manage the growing number of tasks in their various states of revision and trialling, the Harvard Group built a database tailored to this purpose. It incorporates information of task length, the mathematical domains that the task involves, the kinds of mathematical performance actions the task calls for and their relative weights, special materials that may be needed for the execution of the task, and dates and places indicating where and when the task has been trialled.
We gave explicit consideration to a variety of attributes in trying to assemble balanced packets. The overall constraint was set by the assumption that the administration of an entire assessment packet of on-demand tasks should take of the order of ten hours or two weeks of class mathematics time. This figure was arrived at after substantial consultation with teachers, and represents our best effort at conveying their sense of the “doable” and the desirable. It is important to point out that this estimate does not include time spent working on projects. Teachers felt, and we agree with them, that projects could usefully be assigned throughout the school year, either as the focus of mathematics attention in the class or as a parallel ongoing activity.
The ten-hour constraint led to the assembling of packets of on-demand tasks which contain about twenty tasks. About one third of the tasks are problems and the rest short or skills tasks. Balancing along the dimension of task length was done by “eyeball.”
Most of the effort that we devoted to balancing packets was centered on the problem of assembling a group of tasks that, taken as a group, have two properties:
· their demands on performance actions (Modeling/Formulating, Transforming/Manipulating, Inferring/Drawing Conclusions, communicating) are reasonably uniformly distributed, and
· their demands on different mathematical domains (Number and Quantity, Shape and Space, Pattern and Function, Chance and Data, Arrangement) reflect our judgment of the relative importance of that domain for the grade level for which the packet was designed.
To aid in this task, a spreadsheet for aggregating the relative weights of the various tasks was built. The report of the balancing spreadsheet for each of the packets the Harvard Group produced is included in the descriptive material on the packets to be found in Appendix D of this document.
Our mathematical expectations at the elementary level are, as they should be, a subset of the mathematical content knowledge matrix presented in the first section of this report. The purpose of this appendix is to make this relationship clear and explicit.
The elementary mathematical content matrix contains fewer entries in each of its cells. Most notably, the Shape and Space row of the elementary matrix deals largely with “qualitative” or topological properties of shapes rather than “quantitative” or metric properties, and the pattern and function row is largely devoid of the symbolic formalism that one normally associates with algebra in the secondary grades. The Chance and Data row of the matrix makes few, if any, technical demands of the students. Finally, the row of the matrix that describes the mathematics of arrangement is not to be found at all in the elementary matrix.
|
types of objects |
properties of objects |
operations on objects |
semantics of pragmatic use |
|
Number and Quantity integers rationals (fractions, decimals)
measures length area volume time weight |
order betweenness
part-whole relationships
units dimensions
|
arithmetic operations
addition subtraction multiplication division
|
counting or measuring familiar things in the world around us |
|
Shape and Space topological
metric lines/segments polygons circles |
connectedness (one shape or many) enclosure (inside or outside) distance location symmetry similarity |
scaling projection translation rotation reflection covering and tessellating
|
designing and building objects
mapping and traveling |
|
Pattern function (number sequences) arrangement |
input/output
enumeration |
identifying and describing repetitive relationships |
expressing how something depends on another
organizing discrete information |
|
Chance and Data discrete
|
determinism
randomness
|
sampling (by counts)
representing |
dealing with uncertainty
dealing with lack of precision |
Please note that this analysis is about the inherent mathematical richness of asking people to define useful measures. It is not an empirical description of student work.
People seem to approach the “Square-Ness” problem in one of several different ways. By far the most common ways involve comparing the lengths of the sides of the rectangle in some way.
Let us denote the length of a horizontal leg of a rectangle by H and a vertical leg by V. A first attempt at a measure of “square-ness” might then be
![]() .
.
Thus a rectangle with horizontal sides of 6 cm and vertical sides of 2 cm has a “square-ness” of
4 cm,
while a rectangle with horizontal sides of 2 cm and vertical sides of 6 cm has a “square-ness” of
–4 cm.
Is it desirable to have congruent rectangles have different measures of “square-ness?” Probably not. How then might we revise our measure to fix this defect? Suppose we take as our measure of “square-ness”
![]() .
.
Clearly our problem with congruent rectangles is now repaired. However, consider the following problem: Given two rectangles, one with horizontal sides of 6 cm and vertical sides of 2 cm, and the other with horizontal sides of 18 cm and vertical sides of 6 cm. The first has a “square-ness” measure of
4 cm
and the second has a “square-ness” measure of
12 cm.
Is it desirable to have similar rectangles have different measures of “square-ness”?
There is another problem with this definition. If we measure the length of the sides of our rectangles in millimeters rather than centimeters, then the two rectangles in question have “square-ness” measures of
40 mm and 120 mm.
Presumably it would be desirable to have our measure of “square-ness” be such that similar rectangles had the same value of “square-ness” independent of the units in which the lengths of the sides was measured.
How might we revise our measure in order to achieve this goal?
Suppose we take the quantity
![]()
as our measure of “square-ness.” This measure, in one fell swoop, repairs both the problem of similar rectangles not having the same measure and the measure of “square-ness” depending on the units of length which are used to measure the lengths of the sides of the rectangle.
Are we done now? To some extent, this is a matter of taste. This measure of “square-ness” has the peculiar property that the “square-ness” measure of a square is 0. The “square-ness” measure of a very wide and low rectangle approaches 1. Although it is less easy to see, it is also true the “square-ness” measure of a very narrow and tall rectangle approaches 1. Wouldn’t it be nice to have the measure have the property that the “square-ness” of a square is 1 and that of a very elongated rectangle approach 0?
We could define a new measure
![]() .
.
This measure now has the features we would like our measure to have.
Are we done? Not quite. It looks like this measure depends on 2 variables, H and V. Actually, it is possible to rewrite the form of this measure so that it depends on only one variable.
Define the ratio
![]() .
.
Divide numerator and denominator in the expression for “square-ness” by H. Then with the aid of this definition, it is possible to rewrite our measure of “square-ness” as
![]()
There is another line of thinking about this problem. Using the same notation of H and V for the horizontal and vertical sides of the rectangle, some people take the ratio
![]()
directly as a measure of “square-ness.” This measure has the property that it does not depend on the units in which the lengths of the sides are measured. It does, however, suffer, from the following problem:
Consider a rectangle with horizontal sides of 6 cm and vertical sides of 3 cm. According to this measure the “square-ness” the rectangle has “square-ness”
2
while a rectangle with horizontal sides of 3 cm and vertical sides 6 cm has “square-ness”
![]() .
.
Here is a possible resolution of this difficulty. Let us revise the measure so that it is
![]() .
.
The rectangle in question then has “square-ness”
2.5
in both orientations. This measure of “square-ness” has the peculiar property that the “square-ness” of a square is
2.
We can fix this by revising our measure so that it is
![]() .
.
Is this a satisfactory measure?
There are those who would argue that this measure is not yet satisfactory because the “square-ness” measure of very elongated rectangles grows without limit. In addition, although the “square-ness” measure of the square is one under this measure, the “square-ness” measure of any rectangle that is not a square is larger than 1. Wouldn’t it be nicer if the “square-ness” measure of non-square rectangles was smaller than the “square-ness” measure of squares?
Given the proclivity we have (and that we induce in our students) to “simplify” algebraic expressions, some people may choose to write the last measure of “square-ness” in the form
![]()
Clearly, looked at this way one is making a ratio comparison of two areas. What are they?
There are other ways of measuring “square-ness” based on a comparison of areas. For example, suppose one considers the area of the square whose side is H and the area of the square whose side is V. Then a possible measure of “square-ness” is
![]()
This suffers from the same trouble as
![]()
namely that congruent rectangles in different orientations have different measures of “square-ness.” It also suffers from the problem of geometrically similar rectangles having different values of their “square-ness” measures. In the same spirit of revision as we employed earlier we can define a new measure
![]()
This expression is also the ratio of two areas. Is there a nice geometric interpretation of these two areas?
The are several interesting extensions to the “square-ness” task. The first one we look at is the problem of “cube-ness.” Given a collection of rectangular parallelepipeds, can one decide which is the most cube-like?
In our analysis of the “square-ness” problem, we came to the conclusion that there was really only one parameter of importance. In this case, it would appear that the situation is more complicated. However, if we limit ourselves to parallelepipeds with square cross-sections, then the problem is no more complicated than the “square-ness” problem. This is the case for the following reason. Assume the height of the parallelepiped is given by H, and the width and depth by L, then all analyses are likely to lead to some function of the variable H/L.
On the other hand, if we allow all three lengths of the parallelepiped to vary, then we are dealing with a two parameter problem. Measures of “cube-ness” under such circumstances require one to define a function of two variables as an appropriate measure of “cube-ness.”
Another interesting extension of the “square-ness” task is to consider a set of parallelograms instead of a set of rectangles. The initial questions is the same, i.e., which of these figures is the “squarest”? This too, will lead to the necessity for defining a function of two variables as an appropriate measure of “square-ness.” In this case it is likely that one of the variables will be an angle. Possible candidates include the angle between adjacent sides or the angle between the diagonals. Assuming the variable is the ratio of adjacent sides, we have a situation in which one of the variables ranges over an unbounded domain while the other is bounded from both above and below. Alternatively one can regard the angle variable as varying over an unbounded domain, but that the function of two variables that is the measure of “square-ness” is periodic in one of its arguments.
The story doesn’t end here. In fact it probably doesn’t end at all. The moral of the story is that humans make mathematics, and that the problems we pose to our students ought to offer them the opportunity to do the same.
In this appendix we list some of the published works that we have found useful in our work. We do not include much of the general literature on assessment and the need for reform, but focus rather on assessing mathematics performance. It should be noted that the published literature is thin when it comes to the question of assessing secondary and post-secondary material.
Baxter, Gail P., Richard J. Shavelson, Sally J. Herman, Katherine A. Brown, and James R. Valadez. “Mathematics Performance Assessment: Technical Quality and Diverse Student Impact.” Journal for Research in Mathematics Education, 24, 3, (1993): pp. 190-216.
Cain, Ralph W. and Patricia A. Kenney, “A Joint Vision for Classroom Assessment.” The Mathematics Teacher 85, 8, (1992): pp. 612-615.
Charles, Randall I., and Edward A. Silver, eds. Research Agenda for Mathematics Education: The Teaching and Assessing of Mathematical Problem Solving. Hillsdale NJ: Lawrence Erlbaum Associates, 1988.
Kulm, Gerald. Assessing Higher Order Thinking in Mathematics. Washington DC: American Association for the Advancement of Science, 1990.
Kulm, Gerald. Mathematics Assessment: What Works in the Classroom. San Francisco CA: Jossey-Bass, 1994.
Leder, Gilah, ed. Assessment and Learning of Mathematics. Victoria, Australian Council for Educational Research, 1992.
Lesh, Richard and Susan J. Lamon, eds. Assessment of Authentic Performance in School Mathematics. Washington DC: American Association for the Advancement of Science, 1992.
Lester, Frank K. and Diana L. Kroll. “Evaluation: A New Vision.” The Mathematics Teacher 84, 4, (1991): pp. 276-283.
Mathematical Sciences Education Board. Measuring What Counts: A Conceptual Guide for Mathematics Assessment. Washington DC: National Academy Press, 1993.
Mathematical Sciences Education Board. For Good Measure: Principles and Goals for Mathematics Assessment. Washington, DC: National Academy Press, 1991.
Office of Technology Assessment. Testing in American Schools: Asking the Right Questions. Washington DC: Office of Technology Assessment, 1992.
Petit, Marge. Getting Started: Vermont Mathematics Portfolio — Learning How to Show Your Best!. Cabot VT: Cabot School, 1992.
Resnick, Lauren B. and Daniel P. Resnick. “Assessing the Thinking Curriculum: New Tools for Educational Reform” in Changing Assessments: Alternative Views of Aptitude, Achievement and Instruction. edited by Bernard R. Gifford and Mary C. O’Connor, Boston MA: Kluwer Academic Publishers, 1992.
Romberg, Thomas A., ed. Mathematics Assessment and Evaluation: Imperatives for Mathematics Educators. Albany NY: State University of New York Press, 1992.
Rothman, Robert. Measuring Up: Standards, Assessment and School Reform. San Francisco CA: Jossey-Bass, 1995.
Schwartz, Judah L. and Katherine A. Viator, eds. The Prices of Secrecy: The Social, Intellectual and Psychological Costs of Current Assessment Practice, Cambridge MA: Educational Technology Center, Harvard University, .1990.
Webb, Norman L. “Assessment of Students’ Knowledge of Mathematics: Steps Toward a Theory” in Handbook of Research on Mathematics and Learning, edited by Doulas A. Grouws, New York NY: Macmillan, 1992.
Webb, Norman L. and Arthur F. Coxford, eds. Assessment in the Mathematics Classroom. 1993 Yearbook, Reston VA: National Council of Teachers of Mathematics, 1993.
Wiggins, Grant P., Assessing Student Performance: Exploring the Purpose and Limits of Testing. San Francisco CA: Jossey-Bass, 1993.
The packet of Grade 4 Tasks represents approximately 12 hours of balanced mathematical assessment. The packet is organized around the ideas of Mathematical Objects and Mathematical Actions. The Mathematical Objects roughly identify the content domains of Number & Quantity, Shape & Space, Pattern, and Chance & Data.
Tasks which are predominately about Number & Quantity make up about 45% of the package; Pattern, which includes both Function and Arrangement, is 35% of the packet. Shape and Space represent about 15% and Chance & Data about 5%.
The package is also balanced with respect to the Mathematical Actions which students are required to perform. These actions are Modeling/Formulating, Manipulating/ Transforming, Inferring/Drawing Conclusions, and Communicating. Individual tasks will vary in the demands that they make on students with respect to these different actions; however,when aggregated across the entire package, the weightings of these actions are grade-appropriately balanced with a slight emphasis on Manipulating/ Transforming and Inferring/Drawing Conclusions.
The tasks are divided into Short Tasks (S) and Problems (L). For the most part the short tasks, which represent about 25% of the total time allocation of the package, deal with basic understanding of the fundamental mathematics being assessed. They are single-concept, and are designed to assess fundamental mastery levels of manipulative and algorithmic skills. The time demands of these questions vary from 5-30 minutes.
In contrast, the problems are designed to allow students to work in a sustained fashion on a task of some depth. They require students to display inventiveness in bringing together disparate elements of what they know in order to solve the problem, and often there will be more than one correct answer. We expect that each problem will occupy a student or group of students for a class period (35-50 minutes).
Balance Sheet-Grade 4 Packet Tasks:
Domain Process Weights
N/Q S/S F C/D A M/F T/M I/D C
L075-Make a Map 1 2 1 3 2
L076-Fermi Four 1 3 3 1 1
L077-Broken Calculator 1 0 2 3 2
L078-Measure Me 1 2 1 2 2
L079-Trouble with Tables 1 0 4 2 0
L080-Broken Measures 1 2 1 2 1
L081-Coding the Alphabet 1 0 2 2 1
L082-Counting Off 1 2 1 3 3
L083-Network News 0.5 0.5 2 2 3 1
L087-Gardens of Delight 0.5 0.5 1 2 2 1
L088-Piece of String 1 0 2 3 1
L089-Mirror Time 1 0 2 2 1
S087-When's the bus? 1 0 3 1 1
S088-Mixed-Up Socks 0.5 0.5 2 1 2 1
S090-Does It Fit? 0.5 0.5 2 0 2 1
S091-Mirror, Mirror 0.5 0.5 1 2 2 1
S092-Valentine Hearts 1 1 2 2 1
S093-Addition Rings 0.5 0.5 0 2 2 2
S094-Multiplication Rings 0.5 0.5 0 2 2 2
S095-Millie & Mel's 1 2 2 3 2
S096-Shape Up 0.5 0.5 0 2 2 1
Content sums 9.5 3 3.5 1.5 3.5
M/F T/M I/D C
Weights
number/quantity N/Q 8.5 21 20.5 15.5 45%
shape/space S/S 2 5 6 3.5 14%
function F 3 6 8.5 6 17%
chance/data C/D 3 1.5 3 2.5 7%
arrangement A 5.5 5.5 8 4.5 17%
16% 28% 33% 23%
The Grade 10 Packet
The packet of Grade 10 Tasks represents approximately 10 hours of balanced mathematical assessment.
The tasks which are designated as Foundation Tasks are designed to be accessible to any school-leaving young adult, regardless of the formal secondary school mathematics courses they have taken. These tasks are more conceptual and less mechanical than tasks that are usually designated as “Basic Skills” questions. They are constructed to reflect the changing mathematical needs of the world in which these student live and work.
The packet is organized around the ideas of Mathematical Objects and Mathematical Actions.
The Mathematical Objects roughly identify the content domain. They are Number & Quantity, Shape & Space, Function, Chance & Data, and Arrangement.
Tasks which are predominately about Number & Quantity make up about 5% of the package. In the Foundation Tasks we expect all students to be able to reason qualitatively about the order properties of integers, fractions and decimals and to approximate the results of numerical computations. We also expect students to be able to estimate length, weight, area, volume, time and number of objects using universal benchmarks.
Tasks which are predominately about Shape & Space make up about 30% of the package. In the Foundation Tasks we expect all students to be able to scale lengths and to read and interpret lengths and areas from visual representations such as blueprints, maps, floor plans and clothing patterns. We also expect students to be able to locate themselves on a map, as well as to plan and navigate routes.
Tasks which are predominately about Function make up about 40% of the package. In the Foundation Tasks we expect all students to be able to evaluate algebraic expressions, to solve simple equations and inequalities and to be able to read and interpret graphs. We also expect students to be able to model simple dependencies qualitatively and to sketch qualitative graphs of these dependencies.
Tasks which are predominately about Chance & Data make up about 20% of the package. In the Foundation Tasks we expect all students to understand elementary statistical ideas such as average, sample size and distribution, and interpretation of probability as a relative frequency. They should also understand the use of statistical evidence in the communications media.
Tasks which are predominately about Arrangement make up about 5% of the package. In the Foundation Tasks we expect all students be able to generate and enumerate simple permutations and combinations.
The package is also balanced with respect to the Mathematical Actions that students are required to perform in doing the tasks. These actions are Modeling/Formulating, Manipulating/Transforming, Inferring/Drawing Conclusions, and Communicating. Although individual tasks will vary in strengths of the demands that they make on students with respect to these different actions, when aggregated across the entire package the weightings of these actions are well balanced, with a slight emphasis on Inferring and Communicating.
The tasks are divided into Short Tasks (S) and Problems (L).
For the most part, short tasks, which represent about 75% of the time allocation of this assessment package, deal with basic understanding of the fundamental mathematics being assessed. They are also designed to assess minimal mastery levels of mechanical manipulative and algorithmic skills. It is expected that these questions will be done individually by students; the time demands of these questions vary from under 5 minutes to about a half hour.
In contrast, the problems are designed to allow students to work in a sustained fashion on a task of some depth. They require students to display inventiveness in bringing together disparate elements of what they know in order to solve the problem, and it will often be the case that there is no unique correct answer. We expect that each problem might occupy a student or group of students for a class period (45-60 minutes). Students should be expected to solve a rich collection of problems, but not all of them. They should be allowed some measure of choice in the problems they are asked to solve, and should have the opportunity to work on some problems in small groups.
Balance Sheet-Grade 10 Packet Tasks:
Domain Process Weights
N/Q S/S F C/D A M/F T/M I/D C
S001-School Zone 1 1 2 1 2
S006-Scale Charts 1 1 1 1 1
S007-House Plan 1 0 2 0 1
S010-Ford & Ferrari 0.5 0.5 0 2 2 1
S012-Square & Circle 1 0 2 1 1
S033-Dollar Line 1 0 0 2 2
S036-Dinner Date 1 2 2 1 1
S053-Function or Not? 1 1 0 0 3 3
S058-World Oil Consumption 1 2 2 2
S060-Postcards from the Falls 1 0 2 1 1
S064-Two Solutions 1 0 2 3 1
S081-Chance of Survival 1 2 1 3 2
S082-Chance of Rain 1 2 1 2 2
L013-Oops!Glass Top 1 2 2 2 2
L063-Telephone Service 1 2 2 3 4
L065-All Aboard 1 2 3 2 2
L074-Pizza Toppings 1 3 3 2 2
Content sums 1 5.5 6.5 3 1
M/F T/M I/D C
Weights
number/quantity N/Q 2 2 1 1 6%
shape/space S/S 4 10 6 7.5 32%
function F 4 10 15 13.5 38%
chance/data C/D 5 4 7 6 18%
arrangement A 3 3 2 2 6%
17% 27% 29% 28%
The Grade 12 Packets
The packets of Senior Tasks each represent approximately 10 hours of balanced mathematical assessment.
The tasks which are designated as Foundation Tasks are designed to be accessible to any school-leaving young adult, regardless of the formal secondary school mathematics courses they have taken. These tasks are more conceptual and less mechanical than tasks that are usually designated as “Basic Skills” questions. They are constructed to reflect the changing mathematical needs of the world in which these student live and work. The remaining tasks in the packet are more mathematically sophisticated, and assume secondary school mathematics training through Geometry and Algebra II, or their equivalents.
The packet is organized around the ideas of Mathematical Objects and Mathematical Actions.
The Mathematical Objects roughly identify the content domain. They are Number & Quantity, Shape & Space, Function, Chance & Data, and Arrangement.
Tasks which are predominately about Number & Quantity make up about 20% of the package. In the Foundation Tasks we expect all students to be able to reason qualitatively about the order properties of integers, fractions and decimals and to approximate the results of numerical computations. We also expect students to be able to estimate length, weight, area, volume, time and number of objects using universal benchmarks. Beyond these minimal skills, at least some students can be expected to undertake number-theoretic tasks, as well as the more elaborate "Fermi problem" tasks.
Tasks which are predominately about Shape & Space make up about 30% of the package. In the Foundation Tasks we expect all students to be able to scale lengths and to read and interpret lengths and areas from visual representations such as blueprints, maps, floor plans and clothing patterns. We also expect students to be able to locate themselves on a map, as well as to plan and navigate routes. Beyond these minimal skills we expect some students to be able to scale areas and volumes as well as to be familiar with geometric concepts and constructs and to be able to formulate, manipulate and interpret geometric models of situations in the world around them, as demonstrated in the "Ness-Test" tasks.
Tasks which are predominately about Function make up about 25% of the package. In the Foundation Tasks we expect all students to be able to evaluate algebraic expressions, to solve simple equations and inequalities and to be able to read and interpret graphs. We also expect students to be able to model simple dependencies qualitatively and to sketch qualitative graphs of these dependencies. Beyond these minimal skills, we expect some students to be able to formulate and manipulate quantitative algebraic models of the world around them using symbolic, numerical and graphical representations. We expect some students to be able to reason, at least qualitatively, about both rates of change and accumulations of functions.
Tasks which are predominately about Chance & Data make up about 15% of the package. In the Foundation Tasks we expect all students to understand elementary statistical ideas such as average, sample size and distribution, and interpretation of probability as a relative frequency. They should also understand the use of statistical evidence in the communications media. Beyond these minimal skills, we expect some students to be comfortable with the concepts of statistical independence, conditional probability, and exploratory data analysis.
Tasks which are predominately about Arrangement make up about 10% of the package. In the Foundation Tasks we expect all students be able to generate and enumerate simple permutations and combinations. Beyond these minimal skills, we expect some students to be comfortable with iterative and recursive algorithms, discrete modeling, and optimization.
The package is also balanced with respect to the Mathematical Actions that students are required to perform in doing the tasks. These actions are Modeling/Formulating, Manipulating/Transforming, Inferring/Drawing Conclusions, and Communicating. Although individual tasks will vary in strengths of the demands that they make on students with respect to these different actions, when aggregated across the entire package the weightings of these actions are well balanced, with a slight emphasis on Inferring and Communicating.
The tasks are divided into Short Tasks (S) and Problems (L).
For the most part, short tasks, which represent about 25% of the time allocation of the assessment package, deal with basic understanding of the fundamental mathematics being assessed. They are also designed to assess minimal mastery levels of mechanical manipulative and algorithmic skills. It is expected that these questions will be done individually by students; the time demands of these questions vary from under 5 minutes to about a half hour.
In contrast, the problems are designed to allow students to work in a sustained fashion on a task of some depth. They require students to display inventiveness in bringing together disparate elements of what they know in order to solve the problem, and it will often be the case that there is no unique correct answer. We expect that each problem might occupy a student or group of students for a class period (45-60 minutes). Students should be expected to solve a rich collection of problems, but not all of them. They should be allowed some measure of choice in the problems they are asked to solve, and should have the opportunity to work on some problems in small groups.
Balance Sheet- Grade 12 Packet I Tasks:
Domain Process Weights
N/Q S/S F C/D A M/F T/M I/D C
L003-Disc-Ness 1 4 1 2 3
L006-Bouncing Off Walls 1 4 1 3 2
L007-Don't Fence Me In 1 4 1 3 2
L009-Birthday Card 1 1 3 2 2
L014-Gligs & Crocs 1 3 2 2 2
L016-Melons & Melon Juice 1 3 2 2 2
L024-Fermi I 1 4 1 3 2
L027-Initials 1 1 0 3 2
L048-Dog Tags 1 3 2 2 2
L051-The Contest 1 2 2 4 3
S003-L to Scale 1 0 2 1 1
S008-Ostrich & Seahorse 1 0 2 1 1
S011-Egyptian Statue 1 1 3 2 2
S013-Transformation I 1 0 3 1 2
S015-Bathtub Graph 1 4 2 0 3
S024-Books from Andonov 1 2 2 2 2
S031-Alcohol Level 1 0 3 2 1
S038-Larger,Smaller 1 0 2 2 1
S048-Stock Market 1 0 1 2 2
S049-Survey Says 1 2 2 2 3
Content sums 4 6 5 3 2
M/F T/M I/D C
Weights
number/quantity N/Q 8 8 9 7 20%
shape/space S/S 13 10 12 11 30%
function F 9 12 7 10 24%
chance/data C/D 4 5 8 8 16%
arrangement A 4 2 5 4 10%
24% 24% 26% 26%
Balance Sheet-Grade 12 Packet II Tasks:
Domain Process Weights
N/Q S/S F C/D A M/F T/M I/D C
L004-Bumpy-Ness 1 4 1 2 3
L015-Mirror,Mirror II 1 3 2 3 2
L017-Garages & Phones 1 4 2 2 2
L025-Fermi Estimates II 1 4 1 3 2
L026-Triskaidecaphobia 0.5 0.5 1 2 2 1
L049-Bagels or Donuts 1 3 3 3 3
L050-Mastermind 1 2 1 3 2
L054-Compact-Ness 1 4 1 2 3
L058-Blirts & Gorks 1 3 2 2 2
L060-Bicycle Chain II 1 2 2 1 2
S004-Scaling the Stars 1 0 2 1 1
S005-Multifigues 1 0 2 2 1
S009-Shirts & Flags 1 0 3 2 1
S014-Transformation II 1 0 3 1 2
S016-Toilet Graph 1 4 2 0 3
S019-Number Graph 1 1 1 3 1
S039-Smaller,Larger, 1 0 2 2 1
S041-Vacation in Bramilia 1 0 3 2 3
S047-Presidential Popularity 1 0 0 3 4
S050-Cost of Living 1 1 3 2 3
Content sums 3.5 6 6 3 1.5
M/F T/M I/D C
Weights
number/quantity N/Q 7.5 6 8 5.5 17%
shape/space S/S 9 12 11 10 27%
function F 12 14 11 14 32%
chance/data C/D 5 4 7 10 17%
arrangement A 2.5 2 4 2.5 7%
23% 24% 26% 27%
The Senior Honors Packet
The packet of Honors tasks represents approximately 15 hours of balanced mathematical assessment.
The tasks are designed to engage students who can be challenged to deal with sophisticated problems. A secondary school mathematics background which includes Geometry, Discrete Mathematics and Precalculus, or their equivalents, is assumed. A full calculus course is not required. The packet is aimed at student who will be applying to highly-selective colleges and universities.
The packet is organized around the concept of Mathematical Objects and Mathematical Actions.
The Mathematical Objects roughly identify the content domains of Function, Shape & Space, Arrangement, Chance & Data, and Number/Quantity. Tasks which are predominately about Function make up about 40% of the packet, Shape & Space about 25% and Arrangement about 15%; the remaining 20% is devoted to Chance & Data and Number/Quantity.
The Functions problems in the packet, while addressing major topics which appear in pre-calculus and calculus courses, require students to go beyond manipulations and formula. The problems attempt to assess understanding of the major concepts in calculus. All problems require the understanding of more than one representation of central concepts such as function, derivative, integral, sequence, etc. They also assess the ability to connect phenomena to symbolic manipulations or graphs, and they require the communication of thoughtful explanations, preferably in various representations. Some of the tasks take advantage of graphing technology to assess skill level in representation and generalization.
The Shape & Space questions go beyond traditional geometric manipulations and constructions and attempt to assess intuitive understanding of spatial relationships, and the way they can be described algebraically.
The Arrangement tasks require students to develop and apply their understanding of basic counting techniques, combinations and permutations. These tasks do not demand a sophisticated background in combinatorics.
In both the Chance & Data and the Number/Quantity tasks there is the assumption that students will be able to undertake number-theoretic tasks and estimations, and will be comfortable with the concepts of conditional probability and exploratory data analysis.
This package is also balanced with respect to the Mathematical Actions that students are required to perform . These actions may be described as Modeling/Formulating, Manipulating/Transforming, Inferring/Drawing Conclusions, and Communicating. Although individual tasks will vary in the demands that they make with respect to these different actions, the weightings of these actions are well balanced when aggregated across the entire package.
The tasks are designated as Short Tasks (S) and Problems (L). The short tasks, which represent about 15% of the time allocation of this package, deal with basic understanding of the fundamental mathematics being assessed. The time demand for these questions varies from 10-30 minutes. In contrast, the problems are designed to allow students to work in a sustained fashion on a task of some depth. They require students to display inventiveness in bringing together disparate elements of what they know, and it will often be the case that there is no unique correct answer. We expect that each problem might occupy a student or group of students for a full class period (45-60 minutes). Students should be expected to solve a rich collection of problems, but not all of them. They should be allowed some measure of choice in the problems they are asked to solve, and should have the opportunity to work on some problems in small groups.
Balance Sheet-Honors Packet Tasks:
Domain Process Weights
N/Q S/S F C/D A M/F T/M I/D C
L010-Square in Square 0.5 0.5 2 1 4 3
L053-Curvy-Ness 1 3 0 3 2
L085-Local & Global 0.5 0.5 2 3 4 2
L086-Para-Ball-A 1 3 2 3 2
L090-A Run for Two 1 3 1 3 2
L092-On Averages & Curves 1 2 3 3 2
L093-Catenary 0.5 0.5 2 1 3 2
L094-Red Dots, Blue Dots 1 2 2 3 2
L095-Genetic Codes 0.5 0.5 3 2 3 2
L096-Tie Breaker 1 4 1 3 4
L100-Dart Boards .05 0.5 2 1 2 2
L101-Getting Closer 1 1 2 3 1
L104-Boring a Bead 1 4 3 3 2
S103-Chameleon Color 0.5 0.5 1 1 3 1
S104-Sharper Image 1 2 3 3 2
C001-Fermi Area 0.5 0.5 3 2 3 2
Content sums 1.5 4 6.5 2 2
Weights M/F T/M I/D C
number/quantity N/Q 3 3 5 2.5 9%
shape/space S/S 11.5 5.5 12 8.5 25%
function F 14 14.5 20.5 12.5 41%
chance/data C/D 1 0.5 1 1 13%
arrangement A 5.5 4.5 7.5 4.5 12%
26% 20% 34% 20%
The Balanced Assessment Technology Resource Package contains a collection of assessment tasks that are best addressed using computers and graphing calculators. We have prepared this collection of tasks for those teachers who wish to supplement their use of Balanced Assessment Task Packets with tasks that are dependent on the the use of technological tools.
This resource package contains tasks that address issues in the mathematics of number and quantity, the mathematics of shape and space, the mathematics of pattern and function and the mathematics of chance and data. The tasks in the resource package are primarily appropriate to secondary level students, although some may be useful at middle school level.
The technological resources needed to use these tasks are as follows:
Number/Quantity tasks any spreadsheet program
Shape/Space tasks Geometric superSupposer
(limited version supplied)
or
Geometer's Sketchpad
or
Cabri Geometry
Pattern/Function tasks any spreadsheet program
and
any graphing calculator
and
Function Supposer: Symbols & Graphs
(limited version supplied)
or
any graphing software
Chance/Data tasks any spreadsheet program
(data supplied in Microsoft Works format)
The first two problems in the packet are designed to help you decide whether a student is nimble enough with spreadsheets and graphing calculators for them to be reasonably used as assessment environments.
Technology Resource Packet Index
Task No. Task Name Dominant Technology
*T001 More or Less Spreadsheet
T002 Looking Through a Window Graphing Calculator
T003 Full of Beans Spreadsheet
*T004 Look High and Low Spreadsheet
*T005 Center of Population Graph.Software/Spreadsheet
*T006 People & Places Spreadsheet
*T007 Flying High Spreadsheet
*T008 Be Well Spreadsheet
*T009 Average Heights & Weights Spreadsheet
*T010 Gestation & Longevity Spreadsheet
T011 Boards I Spreadsheet
T012 Boards II Spreadsheet
T013 Boards III Spreadsheet
T014 Boards IV Spreadsheet
T015 Twinkle, Twinkle Graphing Calc. or Software
T016 “Equal” Equations Graphing Calc. or Software
T017 Crossing the Axis Graphing Calc. or Software
T018 Catching Up Graphing Calc. or Software
T019 Between-Ness I Graphing Calc. or Software
T020 Between-Ness II Graphing Calc. or Software
T021 Between-Ness III Graphing Calc. or Software
T022 Between-Ness IV Graphing Calc. or Software
T023 Between-Ness V Graphing Calc. or Software
T024 Sum & Product Graphing Calc. or Software
TO25 In Oz We Tryst Geometry Software
T026 Cities and Gas Stations Geometry Software
T027 Three Rubber Bands Geometry Software
T028 Divisions Geometry Software
T029 Detective Stories Geometry Software
T030 Calculator Numbers 4-Function Calculator
T031 Area Upgrade Geometry Software
T032 Always, Sometimes, Never Geometry Software
T033 Orthogonal Circles Geometry Software
T034 Circling Trains Geometry Software
T035 Intersections I Graphing Calc. or Software
T036 Intersections II Graphing Calc. or Software
T037 Short Pappus Geometry Software
T038 Broken Spreadsheet I Spreadsheet
T039 Broken Spreadsheet II Spreadsheet
* Spreadsheet data provided
Last Update: 03/01/2015
Copyright © 2026, The Concord Consortium. All rights reserved.